#concept-pamphlet #todo: I’m not certain of these definitions; this ties into my hesitations w.r.t. tensor definition
What is rank in machine learning? ? Rank is the number of linearly independent rows or columns
What are a few uses of matrices? ?
- representing linear transformations
- handling multi-dimensional data
- solving systems of linear equations
- simplifying computational tasks in quantum mechanics.
Matrix A has dimensions a x b Matrix B has dimensions c x d What are the dimensions are Matrix AB, assuming dot product is a valid operation? ? a x d
Matrix A has dimensions a x b Matrix B has dimensions c x d Which dimensions must be equal for AB to be a valid dot product? ? b and c (AT)T = >> A
(A + B)T = >> AT + BT
Transitive property: (P * Q)T = >> QT * PT
(AT)-1 = >> (A-1)T
Is the identity matrix diagonal? Is the zero matrix diagonal? ? Yes because they both have all their off-diagonal elements as zero
Trace of matrix (tr(A))
??
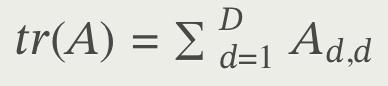 in other words, it is the sum of matrix A’s diagonal elements
in other words, it is the sum of matrix A’s diagonal elements
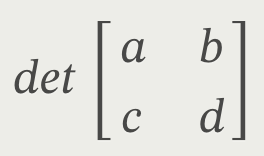 >> ad - bc
>> ad - bc
Visualize the zero matrix >> Matrix of all 0s
Visualize the identity matrix >> Square matrix that is all 0s except on the diagonal. The diagonal is all 1s.
Visualize a symmetric matrix >> If you fold it over the diagonal like origami, it’s the same
Determinant of matrix A (explanation only)
?
Scalar used to calculate the inverse of matrix A

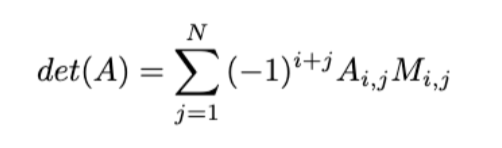 Inverse matrix A^-1 where A is m x n will always be dimensions >> m=n. Square
Inverse matrix A^-1 where A is m x n will always be dimensions >> m=n. Square
A-1 * A = >> A * A-1 = I
(aA)-1 = >> a-1A-1
(AT)-1 = >> (A-1)T
(AB)-1 = >> B-1A-1
what does it mean for two vectors to be orthogonal, equation-wise? ? The condition for two vectors x and y to be orthogonal in an n-dimensional space is defined by the dot product equation: x⋅y=0 or xTy = 0 This equation means that the sum of the products of their corresponding components is zero. Explicitly, if x=(x1,x2,…,xn) and y=(y1,y2,…,yn), then: x1y1+x2y2+…+xnyn=0 This condition must be satisfied for x and y to be orthogonal.
In the context of matrix manipulation, how might the dot product of two vectors a and b be represented? >> ; this results in a scalar which is the dot product
Are vectors by default considered column or row vectors? >> column