MATH 51

#concept-pamphlet #todo: fill with the things that interest me

---

Notes §

Scaffold §

1. Geometry of vectors and projections
2. Multivariate functions and optimizations
3. Geometry and algebra of matrices
4. Matrix algebra and linear systems
5. Eigenvalues and second partial derivatives
6. Pagerank
7. Neural networks and multivariable Chain rule

Intro §

a theorem in mathematics does not become ___ later on as new ideas are discovered. ? false math51book, page 7

read

$$R^3$$

as ? “the set of all triples (x,y,z) of real numbers” math51book, page 8

read

$$\in$$

as ? ‘is in’, ‘is an element of’, ‘belongs to’ read

$$|$$

or

$$:$$

as ‘for which’, ‘such that’

Part I. Geometry of vectors and projections (1-7) §

ch 1 §

Notation §

$$R^n$$

? Set of all n-vectors

$$||v||$$

? length or magnitude of an n-vector v

---

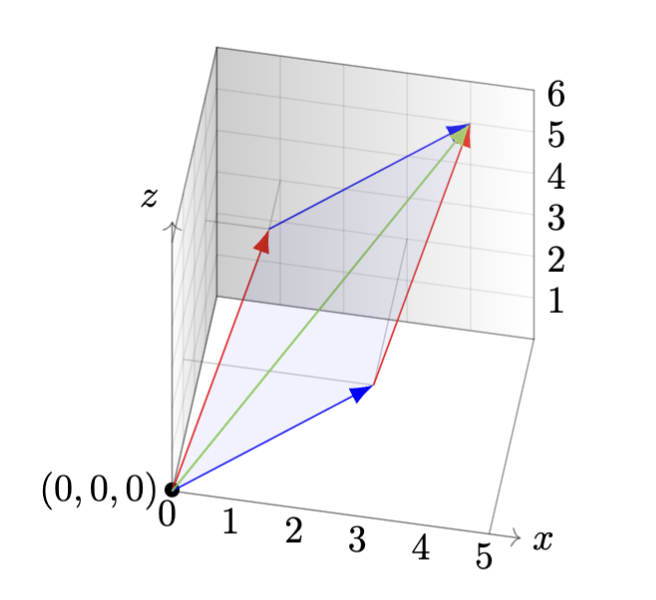
scalar ? a real number visualize 2 n-vectors being added, notation-wise ?

$$\mathbf{a}+\mathbf{b}=\left[\begin{array}{c}{a}_1+b_1\\ a_2+b_2\\ ⋮\\ a_n+b_n\end{array}\right]$$

visualize the shapes of a linear combination ? for given n-vectors $v_1,...,v_k$ and scalars $c_1,...,c_k$ result is n-vector of form $c_1{v}_1+...+c_k{v}_k$ Imagine these vectors being added together in geometric space 💛 ?

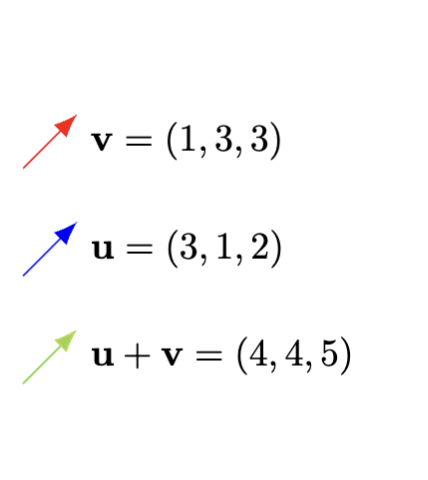convex combination

length

unit vector

---

ch2

correlation coefficient r ? cosine of angle between X and Y … remember the acronym for sine, cosine, tan? >> SOHCAHTOA cosine formula ?

$$cos\theta =\frac{adjacent}{hypotenuse}$$

length via dot product

properties of dot products

verify orthogonality for two n-vectors

---

ch3 points&planessss

ch4 spansslinear subspace 😌 dims

ch5 A collection of vectors $v_1,...,v_k$ in $R^n$ is called orthogonal if ? $v_i\cdot v_j=0wheneveri\ne j$

visualize geometrically, 2 orthogonal vectors in $R^3$ ? when you look at the plane that the 2 vectors are both on, there’s a 90 degree angle (but like…why????? why does this happennnn with dot product) A collection of vectors $v_1,...,v_k$ in $R^n$ is called orthonormal if ? they are orthogonal to each other and are all unit vectors. That is, $v_i\cdot v_i=1$ for all $i$

---

vectors planes in R^3 orthogonality projections linear regression

Part II. Multivariate functions and optimizations (8-12) §

• countour plots
• partial derivatives
• gradients
• gradient descent
• lagrange multipliers
• applications
  • linear programming

Part III. Geometry and algebra of matrices (13-18) §

• derivative matrix
• linear function
• affine function
• matrix multiplication
• markov chains
• matrix algebra applications
• multivariable chain rule
• matrix inverses
• matrix transpose
• orthogonal

Part IV. Matrix Algebra and linear systems (19-22) §

• linear independent

• gram-schmidt process

• orthogonal matrices

• null space

• matrix decompositions

• linear systems

• quadratic form

• qr decomp

• lu decomp

• hessian

• singular value comp

Part V. Eigenvalues and second partial derivatives (23-27) §

• eigenvalues
• eigenvectors
• higher partial derivatives
• applications of eigenvalues
  • singular value decomposition

Part VI. Pagerank §

how it works

Part VII. Neural networks and multivariate chain rule §

a specific example

Part VIII. Cross product §

Part IX. QR algorithm §

Notation §

Concept §

Result §

---

why linear algebra math is important §

• google page rank was combo of eigenvalues and markov chains applied to n-dimensional spaces with N on the order of billions (total number of webpages on the internet)

meta of reading this book §

• blue box = core math concept. don’t skip
• end of each chapter = 1 page summary
• theorem = labeled as such

theorem - mathematical fact which has been proven true

• use special cases and low-dimensional pictures to remember things. Remembering an idea or a visualization is often easier than memorizing a formula, and is a more reliable kind of knowledge.
• definitions are absolutely crucial in mathematics.
• Build up understanding of ideas first in a special case before the general case. After class, read about the material in the book, reread things multiple times, and look through the highlight sum- mary at the end of the chapter. After reading the statement of a result, work out what it is saying in some special cases (e.g., low dimensions, three vectors instead of k vectors, etc.).
• Math can only be learned actively. There is almost no value to looking over notes (or a textbook, or watching a video) and thinking “oh, I can do that; it makes sense”. Watching someone else do a problem, or reading a solution, is wildly different than facing the problem on a blank sheet of paper. One can’t learn to swim by just reading a book, or learn to build a tiled hut from sticks and stones just by watching this video, and likewise math cannot be learned by only watching others do it. In math, all reading must be done with paper and pen/pencil in hand. Instead of just reading worked examples, actively write out solutions on your own.
• Do not blindly memorize things! If the motivation for a definition or the meaning of a result or method is ub. nclear, ask about it.

Two guiding principles in the writing of this book were to give (i) concrete definitions and numer- ical experience before more conceptual perspectives (without diminishing the importance of the latter), (ii) concepts, techniques, and results that are applicable uniformly to R^n for all n (important for many contemporary applications of linear algebra and multivariable optimization across many fields)