#concept
The Chomsky hierarchy contains ___ classes of ___ to describe increasingly complex languages
?
4, formal grammars
The 4 classes of the Chomsky hierarchy, from most complex to simplest.
___enumerable (turing machine)- context-sensitive (turing machine but with finite tape)
____(finite state, finite memory)- regular (finite state)
?
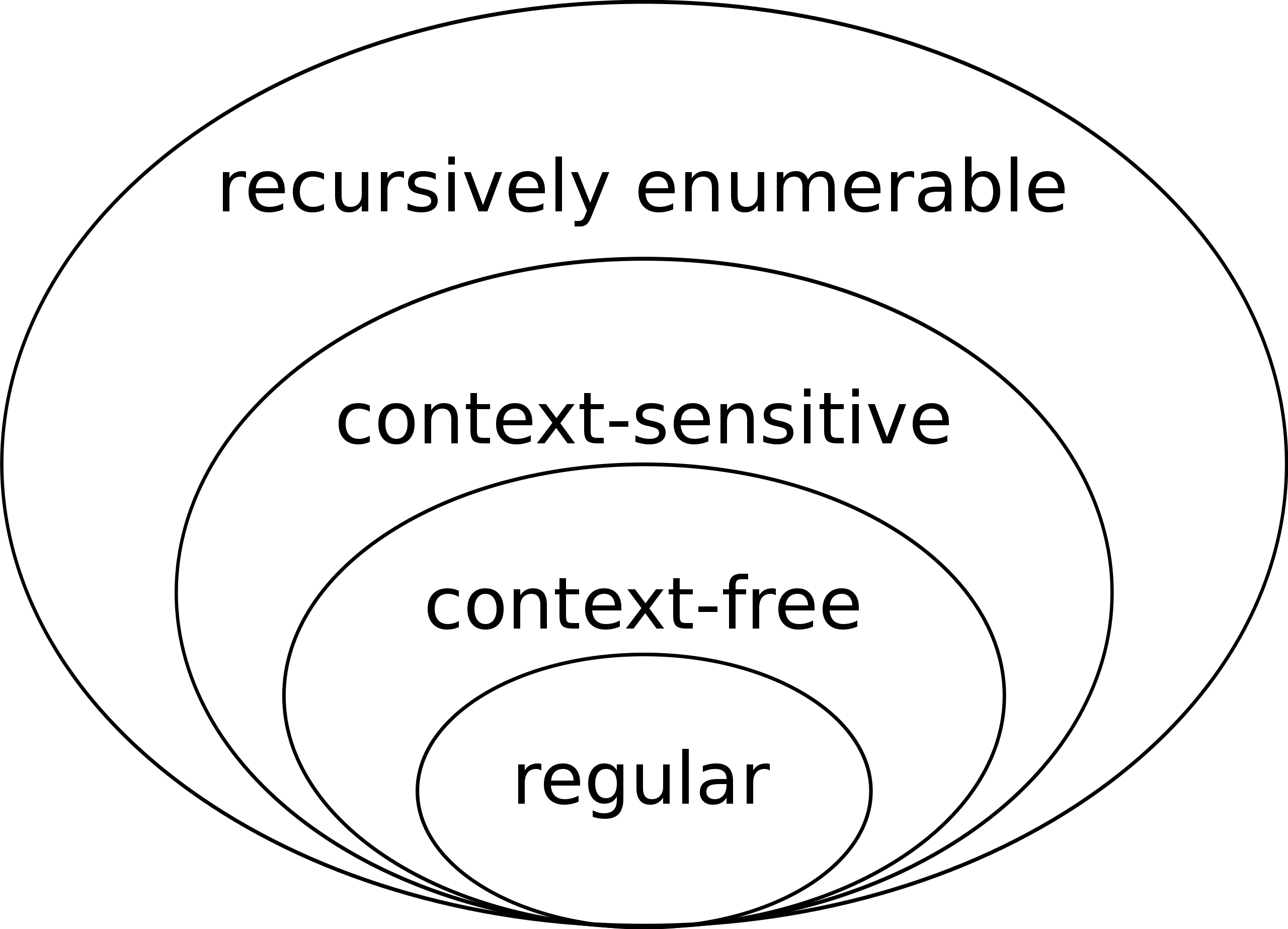In the Chomsky hierarchy, the simplest grammars are regular, and can be accommodated by finite state automata. The next most complicated are context-free grammars, which can be processed by pushdown automata (a device that is a finite state automaton with a finite internal memory). Next are the context-sensitive grammars, which are the domain of linear bounded automata (i.e., a device like a Turing machine, but with a ticker tape of bounded length). The most complex grammars are the phrase structure grammars, which can only be dealt with by Turing machines. [2]
References
- https://en.wikipedia.org/wiki/Chomsky_hierarchy
- http://www.bcp.psych.ualberta.ca/~mike/Pearl_Street/Dictionary/contents/C/Chomhier.html#:~:text=The%20most%20complex%20grammars%20are,theoretical%20proposals%20within%20cognitive%20science.
Notes
children context-sensitive grammar, recursively enumerable grammar, context-free grammar, regular grammar
Self Definition
The Chomsky hierarchy contains 4 classes of formal grammars to describe increasingly complex languages.
Source Definition
The Chomsky hierarchy (infrequently referred to as the Chomsky–Schützenberger hierarchy in the fields of formal language theory, computer science, and linguistics, is a containment hierarchy of classes of formal grammars. A formal grammar describes how to form strings from a language’s vocabulary (or alphabet) that are valid according to the language’s syntax. Linguist Noam Chomsky theorized that four different classes of formal grammars existed that could generate increasingly complex languages. Each class can also completely generate the language of all inferior classes.