#concept-pamphlet #todo: I’m not certain of these definitions; this ties into my hesitations w.r.t. tensor definition
What is rank in machine learning? ? Rank is the number of linearly independent rows or columns
What are a few uses of matrices? ?
- representing linear transformations
- handling multi-dimensional data
- solving systems of linear equations
- simplifying computational tasks in quantum mechanics.
Matrix A has dimensions a x b Matrix B has dimensions c x d What are the dimensions are Matrix AB, assuming dot product is a valid operation? ? a x d
Matrix A has dimensions a x b Matrix B has dimensions c x d Which dimensions must be equal for AB to be a valid dot product? ? b and c
(AT)T = >> A
(A + B)T = >> AT + BT
Transitive property: (P * Q)T = >> QT * PT
(AT)-1 = >> (A-1)T
Is the identity matrix diagonal? Is the zero matrix diagonal? ? Yes because they both have all their off-diagonal elements as zero
Trace of matrix (tr(A))
??
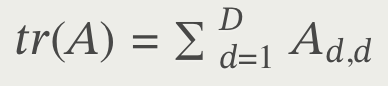in other words, it is the sum of matrix A’s diagonal elements
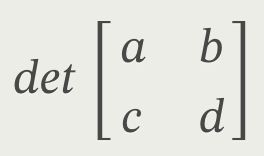>> ad - bc
Visualize the zero matrix >> Matrix of all 0s
Visualize the identity matrix >> Square matrix that is all 0s except on the diagonal. The diagonal is all 1s.
Visualize a symmetric matrix >> If you fold it over the diagonal like origami, it’s the same
Determinant of matrix A (explanation only)
?
Scalar used to calculate the inverse of matrix A
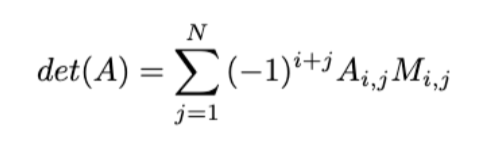Inverse matrix A^-1 where A is m x n will always be dimensions >> m=n. Square
A-1 * A = >> A * A-1 = I
(aA)-1 = >> a-1A-1
(AT)-1 = >> (A-1)T (AB)-1 = >> B-1A-1
what does it mean for two vectors to be orthogonal, equation-wise? ? The condition for two vectors x and y to be orthogonal in an n-dimensional space is defined by the dot product equation: x⋅y=0 or xTy = 0 This equation means that the sum of the products of their corresponding components is zero. Explicitly, if x=(x1,x2,…,xn) and y=(y1,y2,…,yn), then: x1y1+x2y2+…+xnyn=0 This condition must be satisfied for x and y to be orthogonal.
In the context of matrix manipulation, how might the dot product of two vectors a and b be represented? >> aTb ; this results in a scalar which is the dot product
Are vectors by default considered column or row vectors? >> column