#concept-pamphlet #class #todo: weed out the ones I want to keep vs. not
pset 0
?
?
?
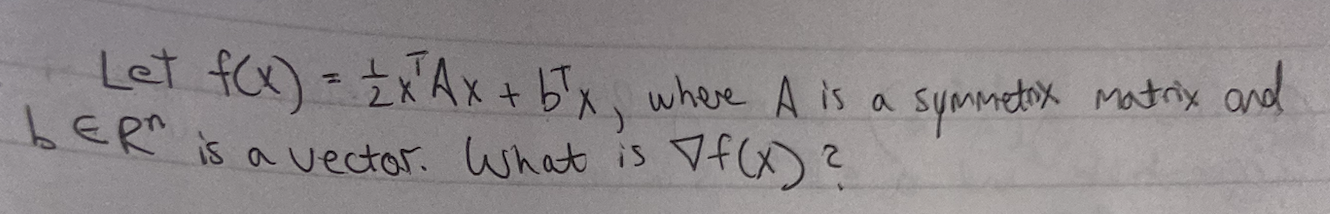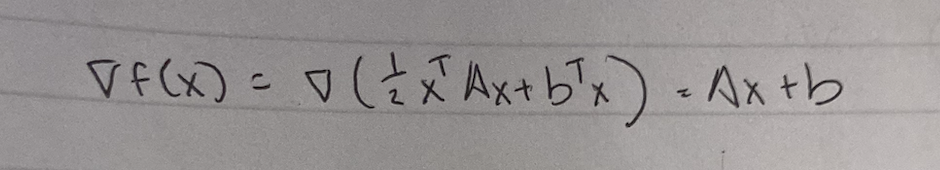
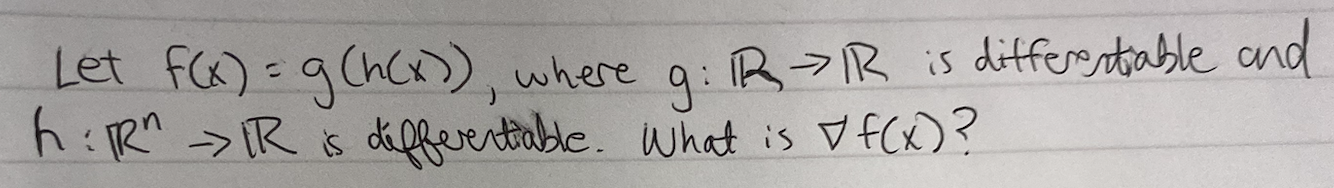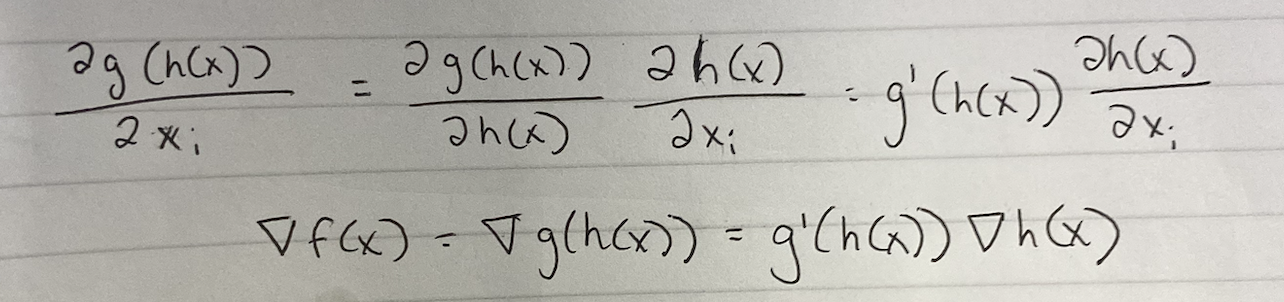
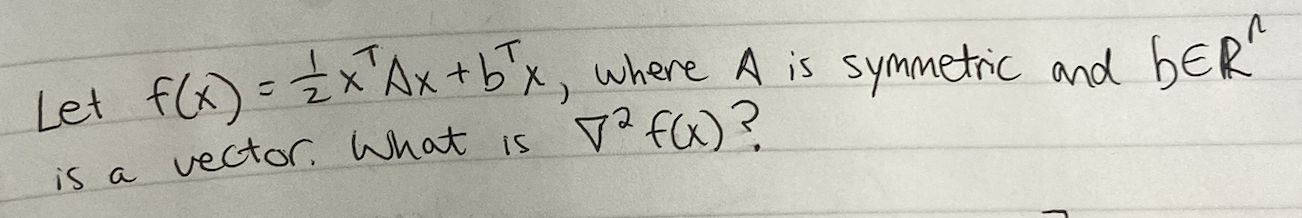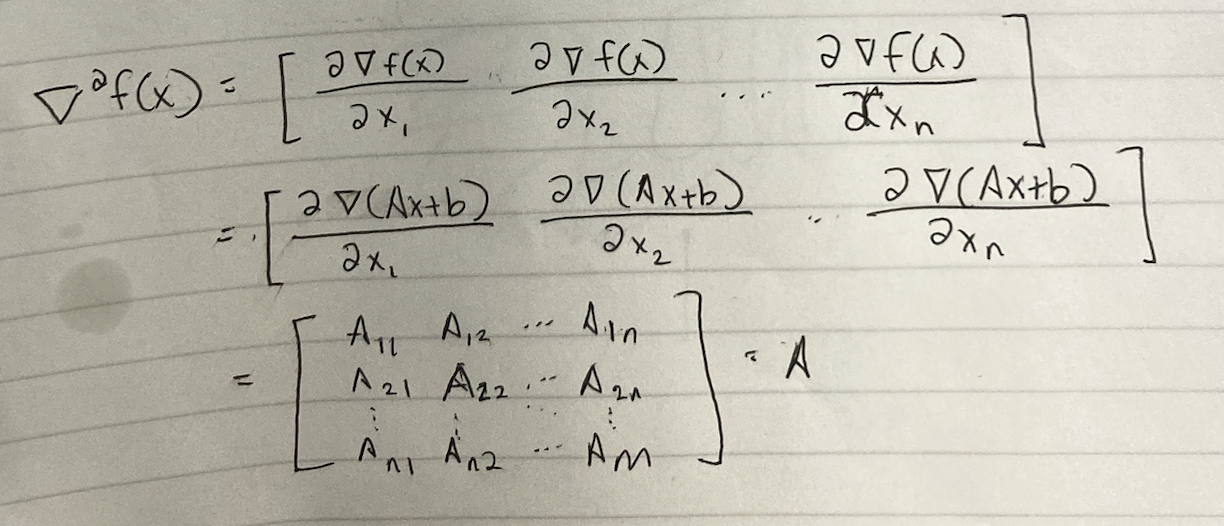
what is an important rule of thumb to keep in mind with matrix multiplication? ? Always think about the dimensions of a given expression
what is a gradient a collection of? what are its dimensions wrt f(x) and x’s dimensions? visualize it. *dimension meaning more similar to rank ? collection of all first order derivatives. if x is n by 1 F() is tensor A by B by C then grad ( F (x) ) is A by B by C by n
what is a hessian a collection of? visualize it ? collection of all second order derivatives.
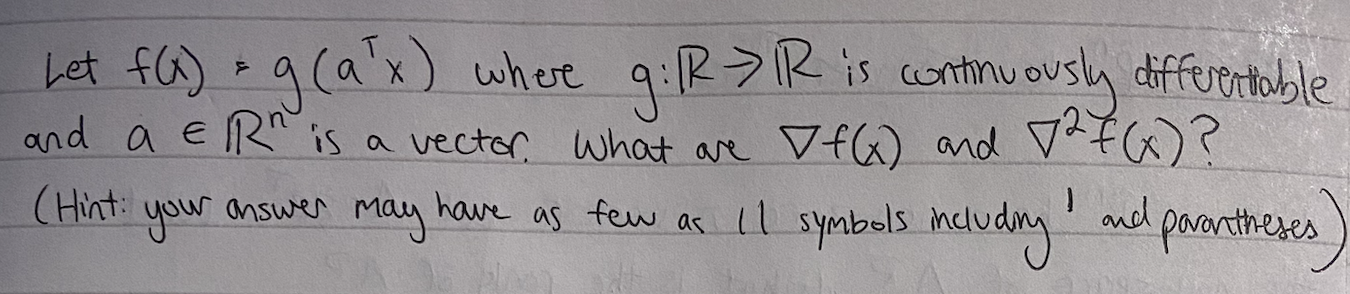hint: think of the dimensions of gradient and hessian, for f: Rn -> R. gradient is nx1. hessian is nxn symmetric matrix
?
?
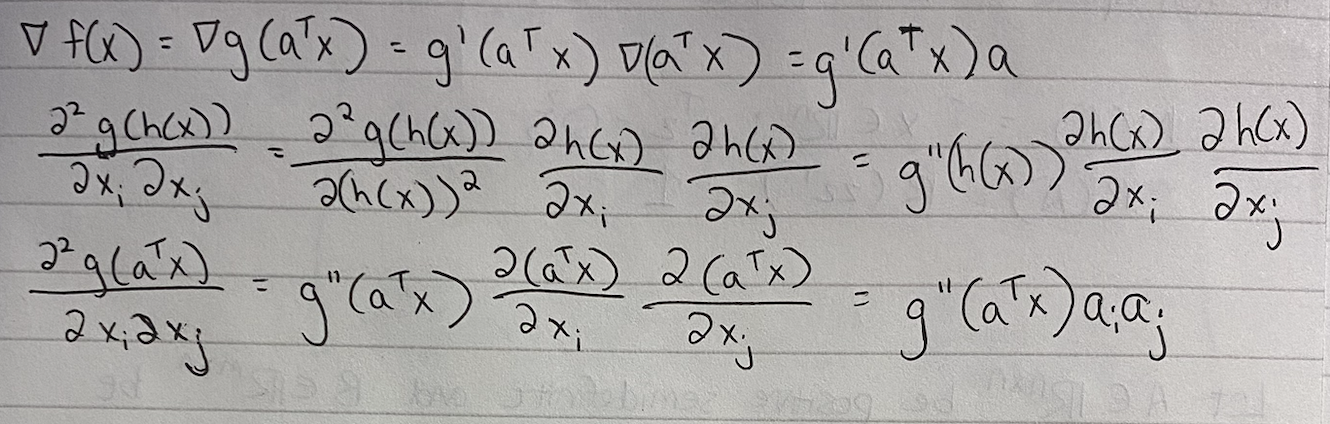
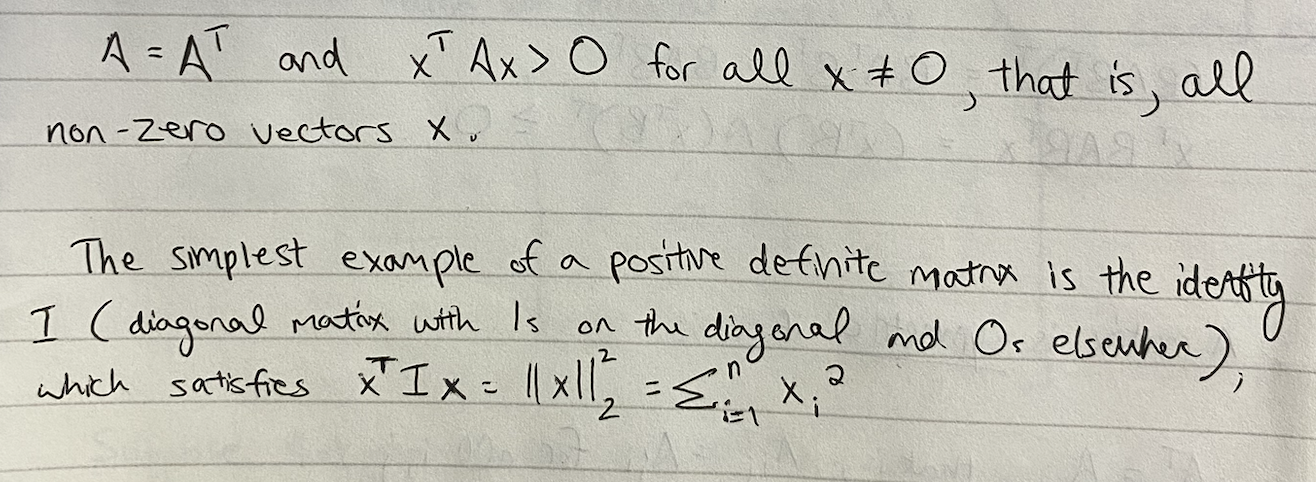TOREVIEW: How is xTAx a possible matmul?
?
?
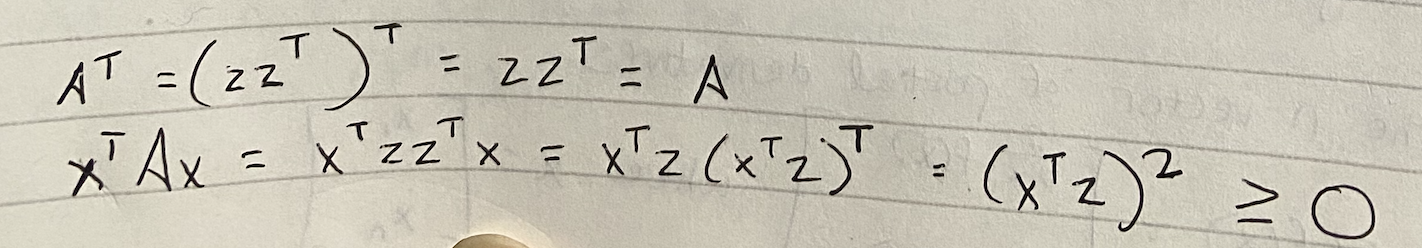
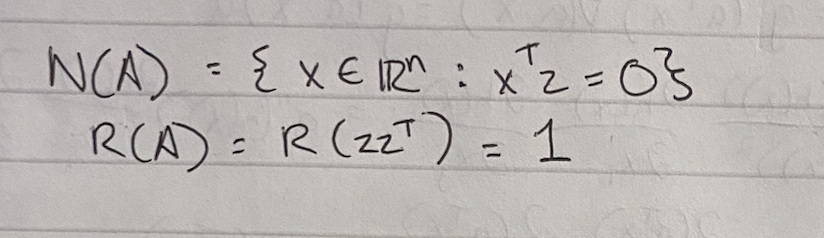TOREVIEW - null space? x^tz = 0? doesn’t x need to be 1xn in shape? isn’t xx^t also rank 2?
?
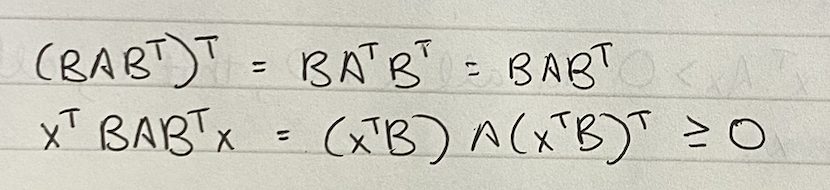it uses the PSD property of A and applies it to BABT!
?
?
?
?
?
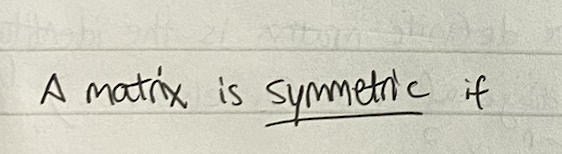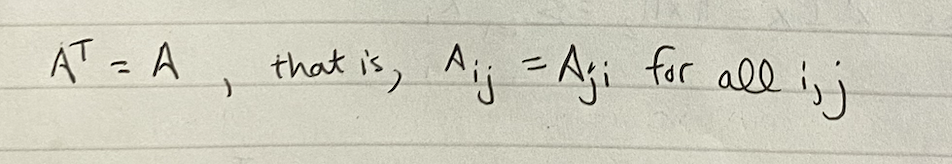
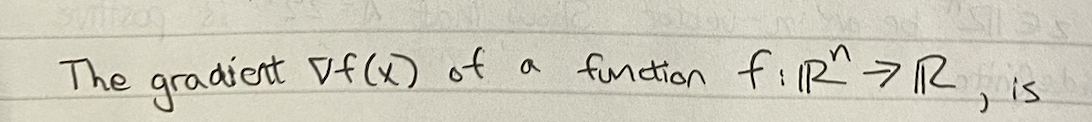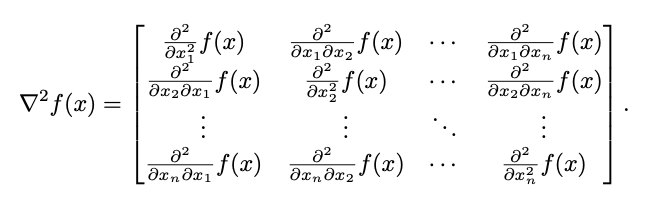
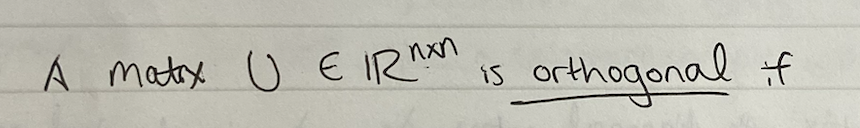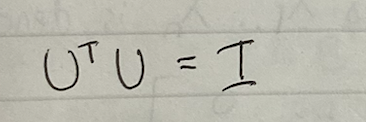
What is rank in deep learning? What rank does a scalar have? ? The rank of a matrix is the maximum number of linearly independent rows or columns in the matrix. For a 2x2 matrix, the rank can be 0, 1, or 2.
- It’s 0 if all elements are zero.
- It’s 1 if the rows (or columns) are proportional to each other (i.e., one row or column is a multiple of the other).
- It’s 2 if the rows (or columns) are linearly independent (i.e., one row or column is not a multiple of the other). The rank gives the number of dimensions spanned by the vectors formed by the rows or columns of the matrix. A scalar has a rank of 0. A vector has a rank of 1, and a matrix can have rank 0, 1, or 2
What is null space in linear algebra? ? A null space (or kernel) of a matrix is the set of all vectors that, when multiplied by the matrix, result in a zero vector. In other words, if A is a matrix, the null space of A consists of all vectors x such that Ax = 0.